Ⅰ. 字符串匹配
字符串匹配问题:字符串 P 是否为字符串 S 的子串?如果是,它出现在 S 的哪些位置? 其中 S 称为主串;P 称为模式串。C语言函数strstr()就是解决字符串匹配的函数,下图为Leetcode 28题,也是解决字符串匹配问题。
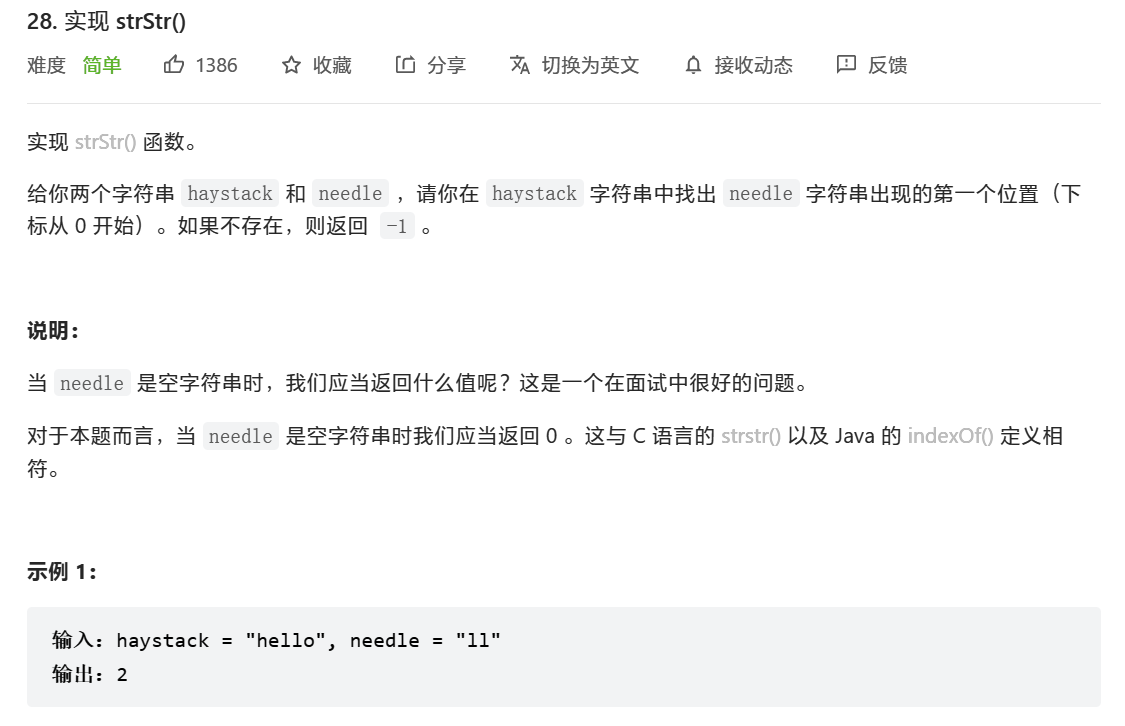
如何去解决字符串匹配问题呢?
Ⅱ. Brute-Force (BF)
按照人脑的第一反应,进行字符串匹配时,从主串的第一个元素开始依次比较连续元素与模式串是否匹配,若出现不匹配则从主串的第二个元素开始,直到找到第一个匹配的位置或者找不到匹配的子串。上述解法也被称为Brute-Force (BF)解法,即暴力解法,也是我们常人能写出来的解法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
int strStr(string haystack, string needle) {
if(haystack.length() < needle.length())
return -1;
if(needle.length() == 0)
return 0;
for(int i=0;i<haystack.length()-needle.length()+1;i++){
int j;
for(j=0;j<needle.length();j++){
if(haystack[i+j]!=needle[j])
break;
}
if(j==needle.length())
return i;
}
return -1;
}
};
PS:实际上使用BF算法已经可以在“LC-28”中AC了,甚至击败了100%的用户。。。。
BF算法理论上时间复杂度为O((m-n)*n)(也可近似为O(m * n),m, n表示主串和模式串的长度,实际过程中消耗的时间要比O((m-n) * n)小)。暴力解法很好理解,但若出现如下情况,这个解法就会变的“很傻”。
- 主串:aaaaaaaaabc
- 模式串:aaab
上述两串进行字符串匹配时,第一次在主串的第3个位置(从0开始)出现不匹配,BF算法的做法既是从主串的第1个位置再重新开始。此时按人脑的思维去看也觉得“很蠢”,因为我们可以一眼看出即使从第1个位置再重新开始也是做无用功,消耗多余的时间和空间,而我们的做法则是直接从第6个位置开始。这也就引出了KMP算法,KMP算法其实就是优化了在出现不匹配后下次开始匹配的位置。
人眼倒是可以直接看出下次开始的位置,那计算机怎么确定下次开始的位置呢?答案是next[]数组。
Ⅲ. KMP
KMP算法的本质其实是动态规划问题,而next[]数组也和dp[]数组有相似性,next[]数组的精髓其实就是充分利用已经匹配的部分。
3.1 next[]
在理解next[]数组前,先要理解前缀、后缀和最长公共前缀。
- 前缀:不包含最后一个字符的所有以第一个字符开头的连续子串。例如:对于字符串 abcxxxxefg,我们称 abc 属于 abcxxxxefg 的某个前缀。
-
后缀:不包含第一个字符的所有以最后一个字符结尾的连续子串。例如:对于字符串 abcxxxxefg,我们称 efg 属于 abcxxxxefg 的某个后缀。
- 最长公共前后缀长度:字符串中前k个字符恰等于后k个字符的最大的k。例如:“aba”中最长公共前后缀为1,“aabaa”中最长公共前后缀为2。
next数组是对于模式串而言的, next 数组就是一个前缀表,next[i]定义为下标为i的元素之前(==包括i==)的子串的最长公共前后缀长度。
- 主串:ababaabaabac
- 模式串:abaabac
也有将next[]数组整体右移一位,即next[0]=-1,思想都是一样的,只是出现不匹配情况时选取next[]的下标不同
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 字符 | a | b | a | a | b | a | c |
| next[i] | 0 | 0 | 1 | 1 | 2 | 3 | 0 |
在清楚手算next[]后,如何使用代码去实现next[]的求解呢?
可分为如下步骤:
- 初始化
- 不匹配
- 匹配
- 更新next[]
1
2
3
4
5
6
7
8
9
10
11
12
13
void getNext(int *next, const string &s){
//初始化定义j为前缀开始位置,i为后缀开始位置
int j = 0;
next[0] = 0;
for(int i = 1; i < s.length(); i++){
//j > 0是为保证j-1不越界,若不匹配则是找前一位的next[]数组,即回退
while(j > 0 && s[i]!=s[j])
j = next[j-1];
if(s[i]==s[j])
j++;
next[i] = j;
}
}
为什么在出现不等时进行回退,并且是找前一位元素的next[]值,这里引用知乎答主阮行止的回答。

3.2 字符串匹配
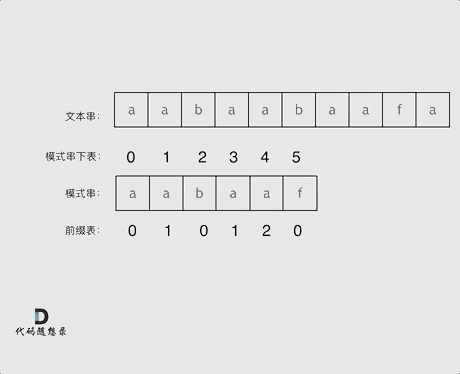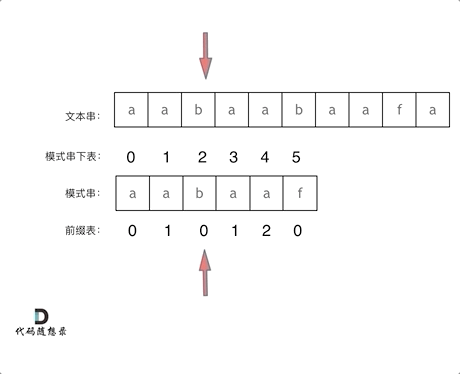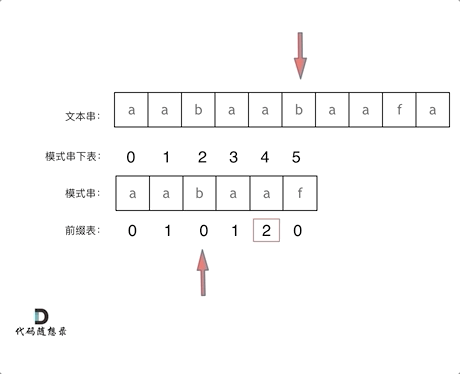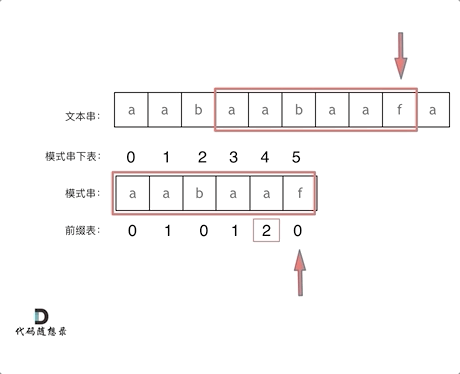
在求取next[]数组后,写出和理解字符串匹配的代码也就简单了,这里借用代码随想录的动图以便更好的理解如何利用next[]数组进行回退以及代码的书写。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int strStr(string haystack, string needle) {
if(haystack.length() < needle.length())
return -1;
if(needle.length() == 0)
return 0;
int next[needle.length()];
getNext(next, needle);
int j=0;
for(int i=0;i<haystack.length();i++){
while(j>0;haystack[i]!=needle[j])
j = next[j-1];
if(haystack[i]==needle[j])
j++;
if(j == needle.length())
return (i-needle.length()+1);
}
return -1;
}
其实可以发现strStr()函数有部分代码和getNext()函数类似,因为用到的思维都是一样的。
除了KMP算法外,还有BM算法以及改进的KMP算法(nextval[]数组),此处不进行记录。