Ⅰ. 推荐课程
【浙江大学】数据结构,浙大的数据结构讲的很精炼,不枯燥易懂,十分适合数据结构的学习。
以下笔记也是根据以该课程为主,并加以具体实现代码。
Ⅱ. 树的定义
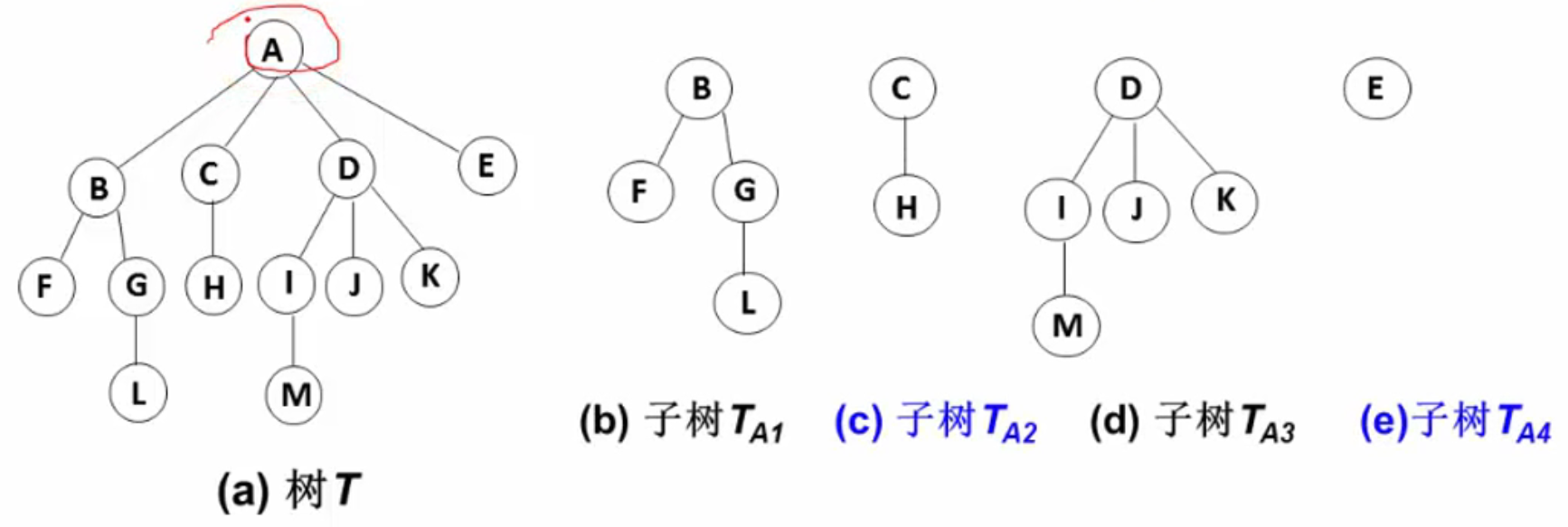
树的定义:是n(n>=0)个结点构成的有限集合。
- n=0时,即没有一个结点,称为空树。
- n>0时,没有双亲结点的唯一结点称为根结点。
- 树由多个子树构成。
- 结点为n的树,其边的数量为n-1(根节点无双亲结点,所以要减一)。
以下均不为树,因为出现了子树相交的情况。
树的一些基本术语:
- 结点的度(Degree):结点的子树个数。
- 树的度:树的所有结点中最大的度数
- 叶结点(Leaf):度为0的结点。
- 父结点(Parent):有子树的结点是其子树的根结点的父结点。
- 子结点(Child):若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子结点。
- 兄弟结点(Sibling):具有同一父结点的各结点彼此是兄弟结点。
- 路径和路径长度:从结点n1到nk的路径为一个结点序列n1,n2,…,nk是ni+1的父结点。路径所包含边的个数为路径的长度。
- 祖先结点(Ancestor):沿树根到某一结点路径上所有结点都是这个结点的祖先结点。
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙。
- 结点的层次(Level):规定根结点在1层,其他任一结点的层数是其父结点的层数加1.
- 树的深度(Depth):树中所有结点中最大层次是这棵树的深度。
Ⅲ. 树的表示
树如果使用单纯的数组进行存储和表示肯定是不行的,因为很难知道树中结点之间的关系。
树中常用的表示方法包括三种:
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法
3.1 双亲表示法
定义数据结构存放树的结点,每个结点含两个域:数据域(存放结点数据)和双亲域(存放双亲结点位置)。
双亲表示法寻找结点的双亲很容易,而寻找结点的子结点很困难。
结点定义
1
2
3
4
typedef struct PTNode{
TElemType data;
int parent;
};
树结构定义
1
2
3
4
5
#define MAX_TREE_SIZE 100
typedef struct PTree{
PTNode nodes[MAX_TREE_SIZE];
int r,n; //根结点的位置和结点个数
};
3.2 孩子表示法
把每个结点的孩子结点排列起来,看成是一个线性表,用单链表作存储,则 n 个结点有 n 个孩子链表(叶子的孩子链表为空表)。而 n 个头指针又组成一个线性表,用顺序表(含 n 个元素的结构数组)存储。
孩子表示法寻找孩子结点很容易,而寻找双亲结点很困难。
孩子结点定义
1
2
3
4
typedef struct CTNode{
int child;
struct CTNode *next;
}*ChildPtr;
双亲结点定义
1
2
3
4
typedef struct CTBox{
TElemType data;
ChildPtr firstchild; //指向孩子的指针
};
树结点类型定义
1
2
3
4
typedef struct CTree{
CTBox nodes[MAX_TREE_SIZE];
int n,r; //结点数和根结点的位置
};
3.3 孩子兄弟表示法
用二叉链表作树的存储结构,链表中的每个结点的两个指针域分别指向其第一个孩子结点和下一个兄弟结点。
孩子兄弟表示法也称为二叉树表示法,容易实现树的各种操作,计算机学科对树的研究也主要是集中在二叉树中。
树结点类型定义
1
2
3
4
5
typedef struct CSNode
{
ElemType data;
struct CSNode *firstchild,*nextsibling; //孩子指针域和兄弟指针域
}CSNode,*CSTree;