Ⅰ. 推荐课程
【浙江大学】数据结构,浙大的数据结构讲的很精炼,不枯燥易懂,十分适合数据结构的学习。
以下笔记也是根据以该课程为主,并加以具体实现代码。
Ⅱ. 并查集
在学习并查集前请先看如下例子,假如有10台电脑(编号为1-10),已知下列电脑之间实现了连接:1和2、2和4、3和5……,问2和7之间是否连通,一共包含多少个连通集?
在解决这个问题前我们需要明白一个特性:电脑的连接具有传递性,即1和2连接,2和3连接,则1和3也连接。
因此根据以上特性,我们可以通过集合进行解决。
- 将10台电脑看成10个单集合
- 若编号为i的电脑和编号为j的电脑连通,则将这两个集合并起来
- 查询编号为i的电脑是否和编号为j的电脑连通,就看这两台电脑是否属于一个集合
- 有多少个集合就有多少个连通集
上述这类问题通过集合进行解决可以使得问题变得很清楚简单,而集合的操作中最长使用的则是并和查,俗称并查集。
集和的表示
集合的表示我们可以使用树的数据结构,选取一个元素作为根结点,使其他的元素指向根结点,存储方式我们采用数组,通过定义一个数据域和指针域表示集合结点。
1
2
3
4
5
#define MaxSize 10 //MaxSize为集合的大小,根据实际情况改变
typedef struct SetType{
ElemType Data;
int Parent;
};
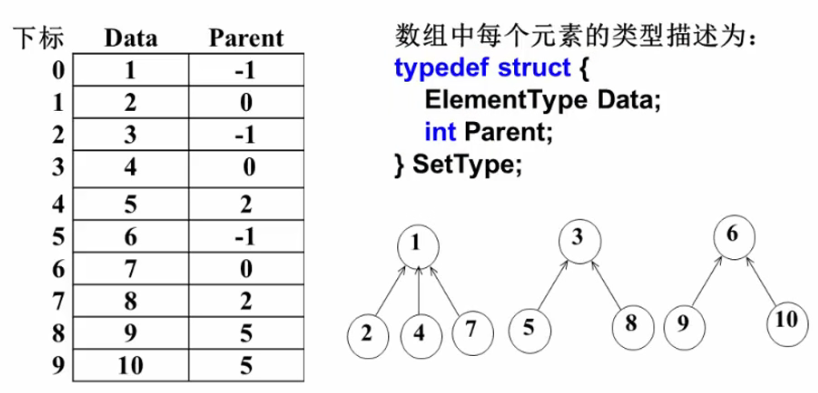
查找元素所在的集合
1
2
3
4
5
6
7
int Find(SetType s[], ElemType x){
for(int i=0;i<MaxSize && s[i]!=x;i++) ;
if(i>=MaxSize)
return -1;
for(;s[i].Parent>=0;i=s[i].Parent) ;
return i;
}
该算法有个缺点,即在进行查找元素所在集合前,先对是否存在该元素进行了查找,该查找是线性的,若数组很长,而元素恰巧又在最后一个,那么消耗的时间是很大的。
集合的简化运算
集合有个特性是集合中的元素是唯一的,那么我们可以利用这个特性对集合的表示进行简化,采用空间换时间的思想,创建足够大的数组,将数组下标表示集合元素,其内容表示根结点,默认为-1。
该情况仅适用于元素均为非负整数的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#define MaxSize 20
typedef int ElemType;
typedef int SetName;
typedef ElemType SetType[MaxSize];
SetName Find(SetType s, ElemType x){
for(;s[x]>=0;x=s[x]);
return x;
}
//并运算
void Union(SetType s, SetName Root1, SetName Root2){
s[Root2] = Root1;
}
按秩归并
为什么需要用到按秩归并?在进行并运算时,我们书写的算法是将root2集合的根结点变更为root1,若多次进行并元素,均为将其他集合的根结点变更为root1,则将会出现树越来越高的情况,从而使得集合退化为类似单链表的结构,效率很慢。
因此在进行并运算时需要进行判断:将矮的树(或为元素少的树)并到高的树上。此时我们只需要将根结点的-1修改为-树高(或-元素个数)即可。
下列演示为树高表示法
1
2
3
4
5
6
7
8
9
10
void Union(SetType s, SetName Root1, SetName Root2){
if(s[Root1] < s[Root2]){
s[Root1] = Root2;
s[Root2]--;
}
else{
s[Roo2] = Root1;
s[Root1]--;
}
}
路径压缩
若出现下图左边的情况,在查找x的根结点时,需要多次上寻,有无办法可以将左边的图转换为右边的图呢?
1
2
3
4
5
6
7
SetName Find(SetType s,ElemType x){
if(s[x] < 0)
return x;
else
return s[x] = Find(s,s[x]);
}
//先找到根,再将根变成x的父结点,z
