数据结构

数据结构—图、图的遍历

[Data Structre] Graphs and Graph Traversals

Posted by PYQ on May 10, 2022

Ⅰ. 推荐课程

【浙江大学】数据结构，浙大的数据结构讲的很精炼，不枯燥易懂，十分适合数据结构的学习。

以下笔记也是根据以该课程为主，并加以具体实现代码。

Ⅱ. 图

图表示“多对多”的关系，当涉及到一点到另外一点的最短路线或最便宜的路线时就需要使用到图。

图的组成：

  • 顶点：通常用V (Vertex) 表示顶点的集合。
  • 边：通常用E (Edge) 表示边的集合。
    1. 边其实是两点的关系
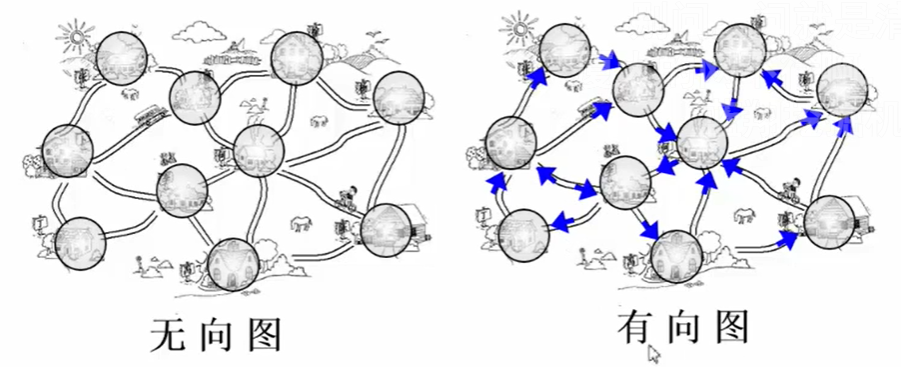
    2. 无向图：$(v, w) \in E, v, w \in V$
    3. 有向图：$<v, w>\in E, v,w \in V$
    4. 图不考虑重边（即两个顶点之间直接相连的仅一条边）和自回路

image-20220510100316462

ADT

1
2
3
4
5
6
7
8
9
10

类型名称：图（Graph）
数据对象集：G(V, E)由一个非空的有限顶点集合v和有限边集合E组成。
操作集：
    Graph Create(); //建立并返回空图
	Graph InsertVertex(Graph G, Vertex v); //将V插入G
	Graph InsertEdge(Graph G, Edge e); //将e插入G
	void DFS(Graph G, Vertex v); //从顶点v出发深度优先遍历图G
	void BFS(Graph G, Vertex v); //从顶点v出发广度优先遍历图G
	void ShortestPath(Graph G, Vertex v, int Dist[]); //计算顶点v到其他任意顶点的最短距离
	void MST(Graph G); //计算最小生成树

Ⅲ. 图的表示

3.1 邻接矩阵表示法

邻接矩阵表示法即使用一个N*N的矩阵表示一个具有N个顶点的图。

若G[i] [j] = 1，则表示图G中顶点i和顶点j存在边；若为0则表示两顶点不连通。

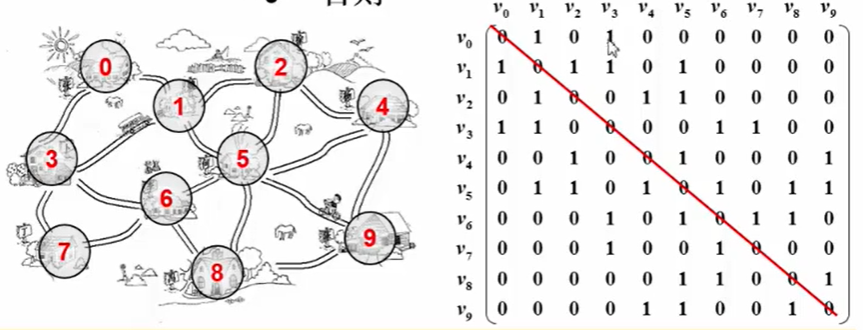
image-20220510101624517

上图展示了使用邻接矩阵表示无向图，可以看到对角线均为0（因为图不允许出现自回路），上三角矩阵和下三角矩阵是完全对称的。

因为上三角矩阵和下三角矩阵是完全对称的，因此我们对于无向图，我们仅存储一半元素即可。

方法：使用一个长度为N(N+1)/2的一维数组存储，G[i] [j]的下标则为(i*(i+1)/2 + j)。

邻接矩阵的好处：

  • 直观、简单、好理解
  • 方便检查任意一对顶点之间是否存在边
  • 方便找任意顶点的所有邻接点
  • 方便计算任一顶点的度（包括入度和出度）

邻接矩阵的缺点：

  • 不适合稀疏图（点多边少），浪费空间
  • 在统计稀疏图中一共有多少边很麻烦

3.2 邻接表表示法

邻接表表示法即使用一个链表数组来表示图，G[N]为指针数组，对应矩阵每行一个链表，只存非0元素，表示与该点邻接的点。

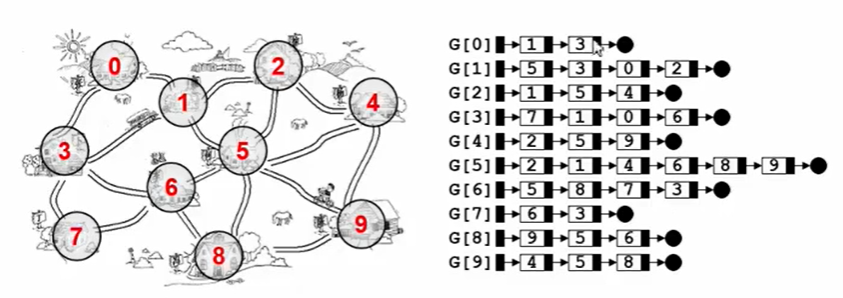
image-20220510103631300

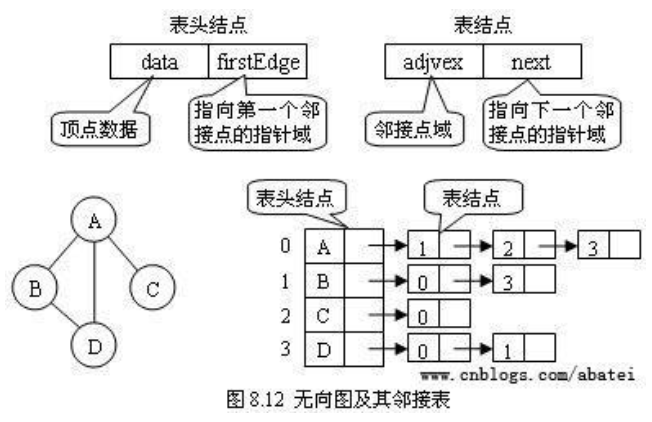
邻接表的优缺点：

  • 方便找任一顶点所有的邻接点
  • 适合稀疏图
  • 对于无向图，适合计算任一顶点的度，而对于有向图，则只能计算“出度”。

image-20220510110751888

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

/*邻接表结构*/
typedef char VertexType;     //顶点类型 
typedef int EdgeType;		//权值类型 
 
/*边表结点*/ 
typedef struct EdgeNode
{
	int adjvex;      	 	//邻接点域,保存邻接点下标    
	EdgeType weight;		//存储权值，非网图则不需要 
	struct EdgeNode *next;	//链域，指向下一个邻接点 
}EdgeNode;
 
typedef struct VertexNode
{
	VertexType data;       	//顶点域 
	EdegeNode *firstedge;	//边表头指针	
}VertexNode,AdList[MAX];
 
typedef struct
{
	AdjList adjList;
	int numVertexes,numEdges;    //顶点数量和边数量 
}GraphAdjList,*GraphAdj;

创建邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/*邻接表创建*/
void create(GraphAdj G){
	int i,j,k;
	EdgeNode *e;
	printf("输入顶点数,边数：");
	scanf("%d%d",&G->numVertexes,&G->numEdges);
    //建立顶点表
	for(i=0;i<G->numVertexes;i++){
		scanf("%c",&G->adjList[i].data);
		G->adjList[i].firstedge=NULL; 		//注意将边表置空 
	}
    //建立边表
	for(k=0;k<G->numEdges;k++){
		printf("输入边(Vi,Vj)上的顶点序号：");
		scanf("%d%d",&i,&j);
		/*使用头插法加入边表结点*/
		e=(EdgeNode *)malloc(sizeof(EdgeNode));   //生成边表结点 		
		e->adjvex=j;
		e->next=G->adjList[i].firstedge;
		G->adjList[i].firstedge=e;
	    
        //此处很关键，因为邻接表中的边其实是创建了两次的
		e=(EdgeNode *)malloc(sizeof(EdgeNode));   //生成边表结点 		
		e->adjvex=i;
		e->next=G->adjList[j].firstedge;
		G->adjList[j].firstedge=e;				
	} 	 
 }

Ⅳ. 图的遍历

图的遍历分为深度优先遍历（DFS）和广度优先遍历（BFS），原理和树的遍历类似，即通过栈和队列实现。

4.1 DFS

DFS的实现实际是一个递归操作，即从起点出发，对其邻接点依次做DFS，直到所有邻接点均已被访问。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

//邻接表的深度优先递归
void DFS(GraphAdj G,int i){
	EdgeNode *p;
	visited[i]=TRUE;         		//访问过了该顶点，标记为TRUE 
	printf("%c",G->adjList[i].data);
	p=G->adjList[i].firstedge;     //让p指向边表第一个结点
    //在边表内遍历 
	while(p){
		if(!visited[p->adjvex])    //对未访问的邻接顶点递归调用 
			DFS(G,p->adjvex);    
		p=p->next;
	}
 } 
 
//邻接表的深度遍历操作 
void DFSTraverse(GraphAdj G)
{
	int i;
	for(i=0;i<G->numVertexes;i++)
		visited[i]=FALSE;         //初始设置为未访问 
	for(i=0;i<G->numVertexes;i++)
		if(!visited[i])
			DFS(G,i);	//对未访问的顶点调用DFS，若是连通图只会执行一次 			
}

4.2 BFS

图的广度优先遍历和树的BFS类似，即先将初始点的所有邻接点进行遍历并入队（即先访问入队），当一个顶点的所有邻接点都遍历完成后将其出队，依次重复该过程，直到所有顶点均被遍历。

采用循环队列进行实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

void InitQueue(LQueue &Q){  //初始化队列 
	Q->front = Q->rear = 0;
}
 
bool QueueisFull(LQueue &Q){ //判断队列是否满了 
	if((Q->rear + 1) % MAX == Q->front){
		return true;  //已满 
	}
	else{
		return false;
	}
}
 
bool QueueisEmpty(LQueue &Q){//判断队列是否为空 
	if(Q->front == Q->rear){
		return true;
	}
	return false;
}
  
void EnQueue(LQueue &Q, int i){ //入队列 
	if(!QueueisFull(Q)){
		Q->data[Q->rear] = i;
		Q->rear = (Q->rear + 1) % MAX;  //队尾指针后移 
	}
}
 
void DeQueue(LQueue &Q, int *k){ //出队列 
	if(!QueueisEmpty(Q)){
		*k = Q->data[Q->front];
		Q->front = (Q->front + 1) % MAX; 
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

/*广度优先遍历*/
void BFS(GraphAdj G){
	Queue *Q =(LQueue)malloc(sizeof(Queue));
	for(int i = 0; i < G->numVertexes; i++){
		visited[i] = FALSE;
	}
	InitQueue(Q);  //初始化队列 
	for(int i = 0; i < G->numVertexes; i++){
		visited[i] = TRUE;
		printf("\t%c", G->adjList[i].data);
		EnQueue(Q, i);
		
		while(!QueueisEmpty(Q)){
			DeQueue(Q, &i);  
			EdgeNode *e = G->adjList[i].firstedge;  //i顶点的邻接链表的第一个结点
			while(e){//e存在时，将e的所有邻接点加入队列,也就是遍历i的所有邻接点 
				if(!visited[e->adjvex]){ // adjvex是e所表示的结点下标 
					visited[e->adjvex] = TRUE;
					printf("\t%c", G->adjList[e->adjvex].data);
					EnQueue(Q, e->adjvex); //将该结点入队 
				}
				e = e->next; //遍历i的下一个邻接点 
			}
		} 
	}
}
CATALOG
    FEATURED TAGS
    life cloud native OS 数据结构 xv6 Linux docker Git os security security
    FRIENDS