数据结构—二叉树的定义、存储结构和遍历

Ⅰ. 推荐课程

【浙江大学】数据结构，浙大的数据结构讲的很精炼，不枯燥易懂，十分适合数据结构的学习。

以下笔记也是根据以该课程为主，并加以具体实现代码。

Ⅱ. 二叉树的定义

二叉树：

1. 二叉树是有穷结点的集合
2. 二叉树可为空。
3. 二叉树若不为空，则由根结点，其左子树和右子树的两个不相交的二叉树构成。
4. 二叉树的子树也为二叉树。

二叉树可以由如下5种基本形态：空、只有根节点，只有左子树，只有右子树，左右子树都有。

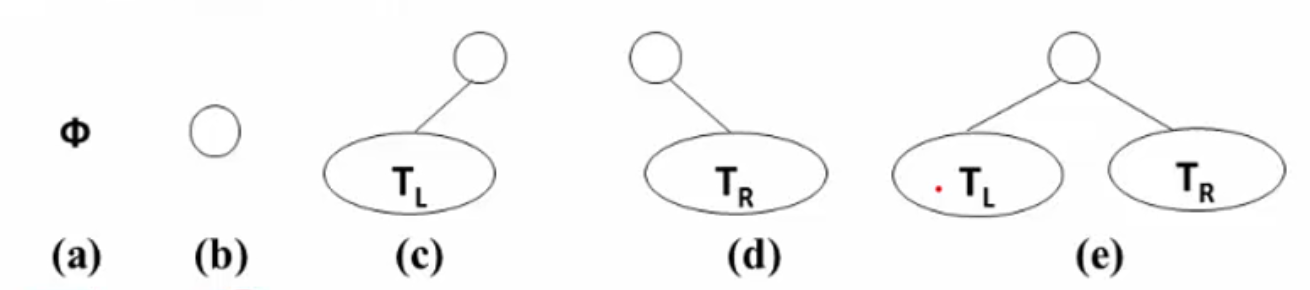
特殊的二叉树

1. 完美二叉树（满二叉树）：除叶子结点外，其他结点的度均为2。

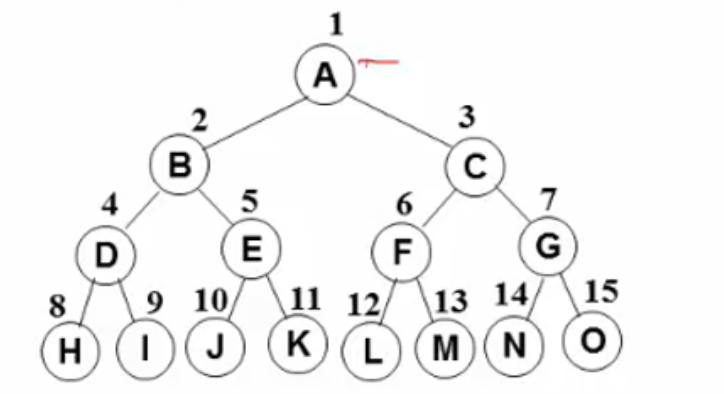
2.完全二叉树：有n个结点的二叉树，对树中结点按从上至下、从左至右的顺序进行编号，编号为i的结点与满二叉树中编号为i的结点在二叉树中位置相同。

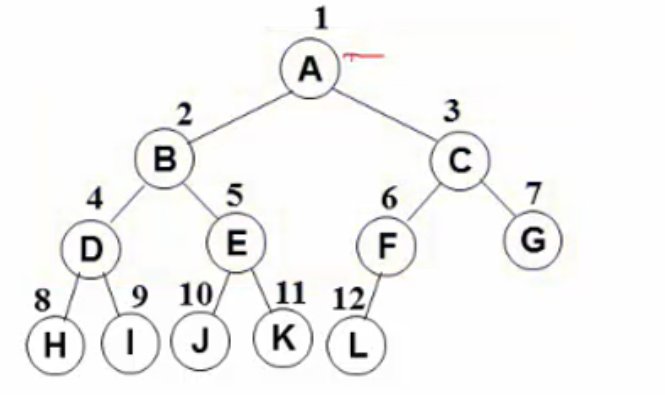
二叉树的性质

1. 一个二叉树第i层的最大结点数为：$2^{i-1}，i>=1$。这个很好理解，公比为2的等比数列。
2. 深度为k的二叉树有最大结点总数为$2^k-1，k>=1$。这个也很好理解，等比数列的求和公式。
3. 对于非空二叉树T，若$n_0$表示叶节点的个数，$n_2$表示度为2的结点个数，则$n_0 = n_2 + 1$。证明如下：树中边的数量等于结点个数之和-1，度为$n$的结点所能提供的边数为$n$。

Ⅲ. 二叉树的存储结构

顺序存储结构：从上至下，从左至右顺序存储n个结点的完全二叉树的结点父子关系；非完全二叉树将缺少的结点赋值为null即可，这种存储结构浪费空间很严重。

以下i均大于1。

• 序号为i的非根结点的父结点的序号为int(i/2)
• 序号为i的结点的左孩子结点的序号为2i（2i<=n，否则无左孩子结点）
• 序号为i的结点的右孩子结点的序号为2i+1（2i+1<=n，否则无左孩子结点）

链表存储结构：结点包括三个元素，数据，左孩子结点，右孩子结点。

1
2
3
4
5
6
7
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
    ElemType Data;
    BinTree Left;
    BinTree Right;
};

Ⅲ. 二叉树的遍历

二叉树的遍历一共包括四种：

1. 先序遍历：根结点，左子树，右子树
2. 中序遍历：左子树，根结点，右子树
3. 后序遍历：左子树，右子树，根结点
4. 层次遍历：从上至下，从左至右

先序遍历

1
2
3
4
5
6
7
void PreOrderTraverse(BTree T){
    if(T==NULL)
        return ;
    printf("%c ",T->Data);
    PreOrderTraverse(T->Left);
    PreOrderTraverse(T->Right);
}

中序遍历

1
2
3
4
5
6
7
void InOrderTraverse(BTree T){
   if(T==NULL)
       return ;
   InOrderTraverse(T->Left);
    printf("%c ",T->Data);
   InOrderTraverse(T->Right);
}

后序遍历

1
2
3
4
5
6
7
void PostOrderTraverse(BiTree T){
    if(T==NULL)
        return;
    PostOrderTraverse(T->Left;
    PostOrderTraverse(T->Right);
    printf("%c ",T->Data);
}

以上为递归实现，若要使用非递归实现则需要利用堆栈，这也是栈的应用之一。

而层次遍历则需要用到队列，先入队，再出队，再将其左右孩子入队，再进行同样的步骤。

• Previous
  数据结构—KMP模式匹配算法
• Next
  数据结构—树的定义和表示